Variational Optimal Transport Methods for Nonlinear Filtering

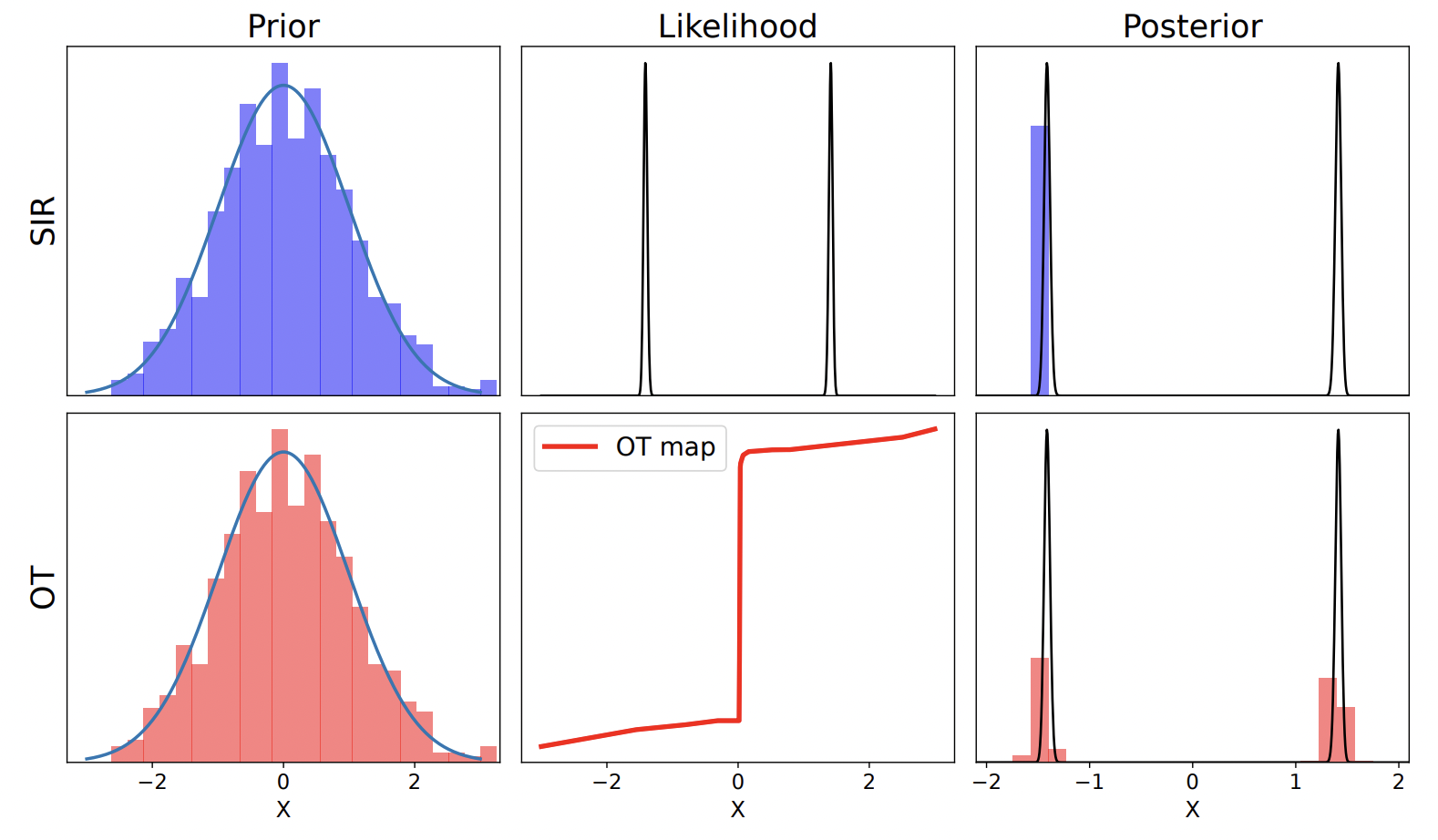
Quantifying uncertainty and effectively assimilating noisy sensory data is is the subject of nonlinear filtering, and is crucial for the reliable and safe operation of control systems. This research project aims to merge recent developments in machine learning (ML) and optimal transportation (OT) to construct nonlinear filtering algorithms with increased flexibility, scalability, and adaptability. This is achieved through the utilization of a novel variational formulation of Bayes’ law, rooted in OT theory, which enables the application of ML tools.

Research supported by the National Science Foundation (NSF) award EPCN-2318977.

Publications:

Presentations:

Fundamentals of Power Generation from Thermal Anisotropy - A Stochastic Control Framework

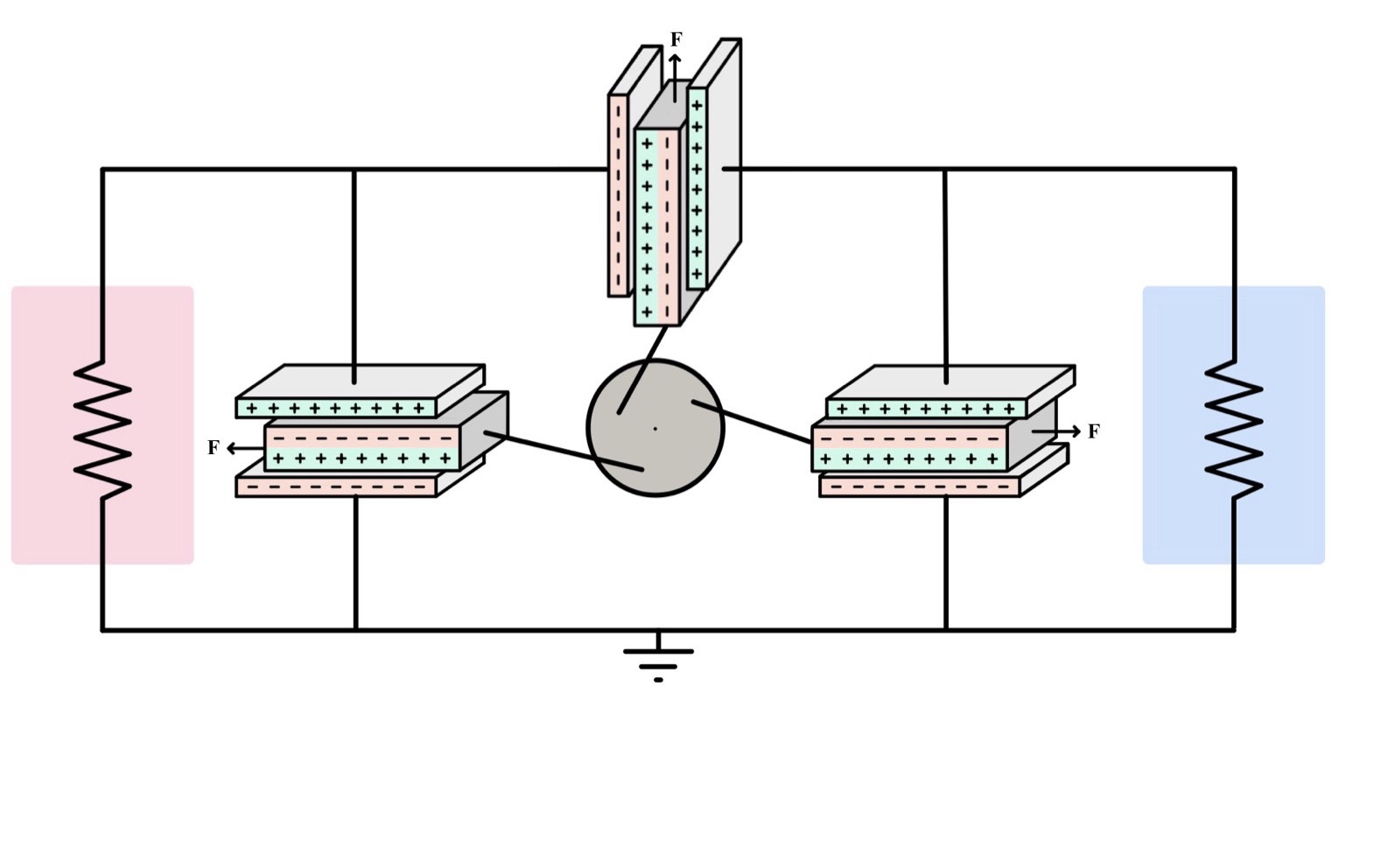
The proposed research is motivated by the central role that anisotropy plays for power generation in physical and engineered processes. On earth, life is sustained by the anisotropy in temperature between the hot Sun and the cold starry sky that fuels an enormous cascade of processes; in hot springs and hydrothermal vents, microorganisms thrive on the temperature and chemical variations they experience; and in living cells, enzymes and molecular motors produce work by tapping onto periodic potentials in polymers, fueled by ATP (adenosine triphosphate) hydrolysis. While it is of great interest to know how Darwinian evolution has tuned such an array of complex processes, our proposed research focuses on functioning principles in utilizing anisotropy in engineered and naturally occurring thermal systems.

Research supported by the National Science Foundation (NSF) award EPCN-2347358.

Publications:

Computational optimal transport, Wasserstein flow, and Sampling

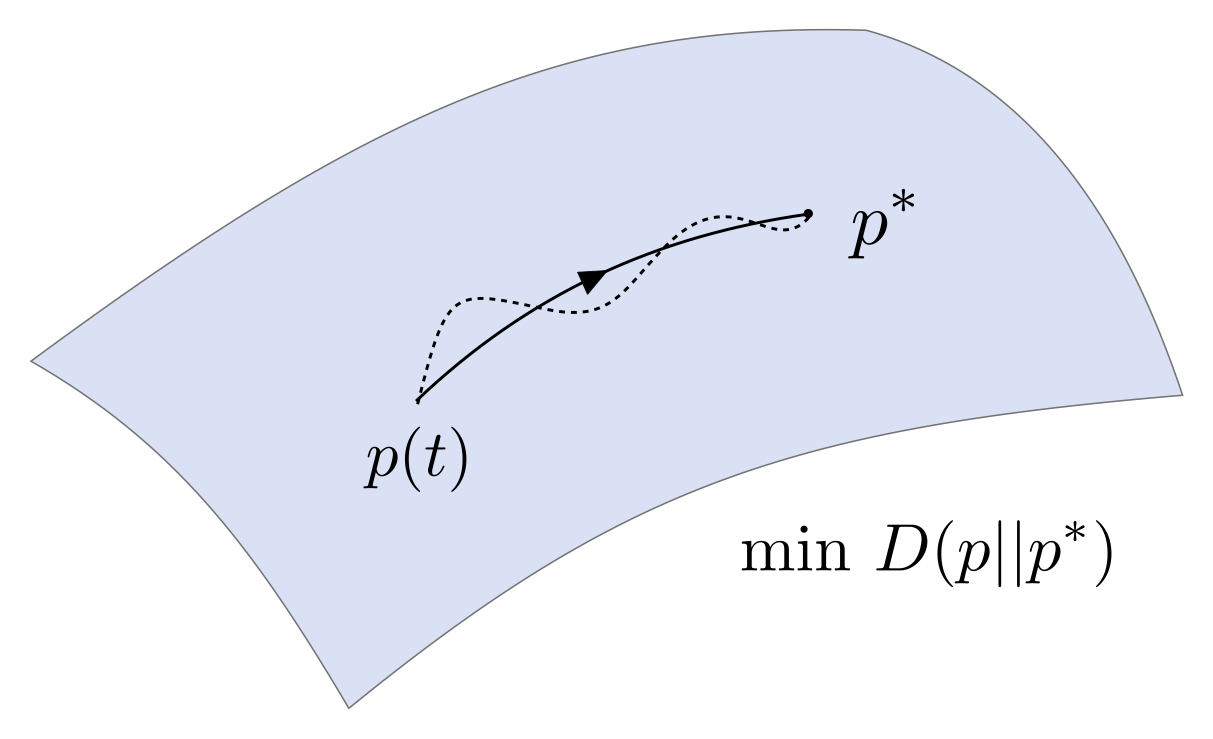
There is a growing interest in application of the optimal transportation theory in machine learning and control related problems. The main reason is that the optimal transportation theory provides powerful and elegant geometrical tools to view and manipulate probability distributions. The objective of this ressearch is to develop efficient data-driven computational algorithms that provide reliable approximations to these geometrical tools in high dimensions.

Publications:

Controlled Interacting Particle Systems for Nonlinear Filtering and Optimal Control

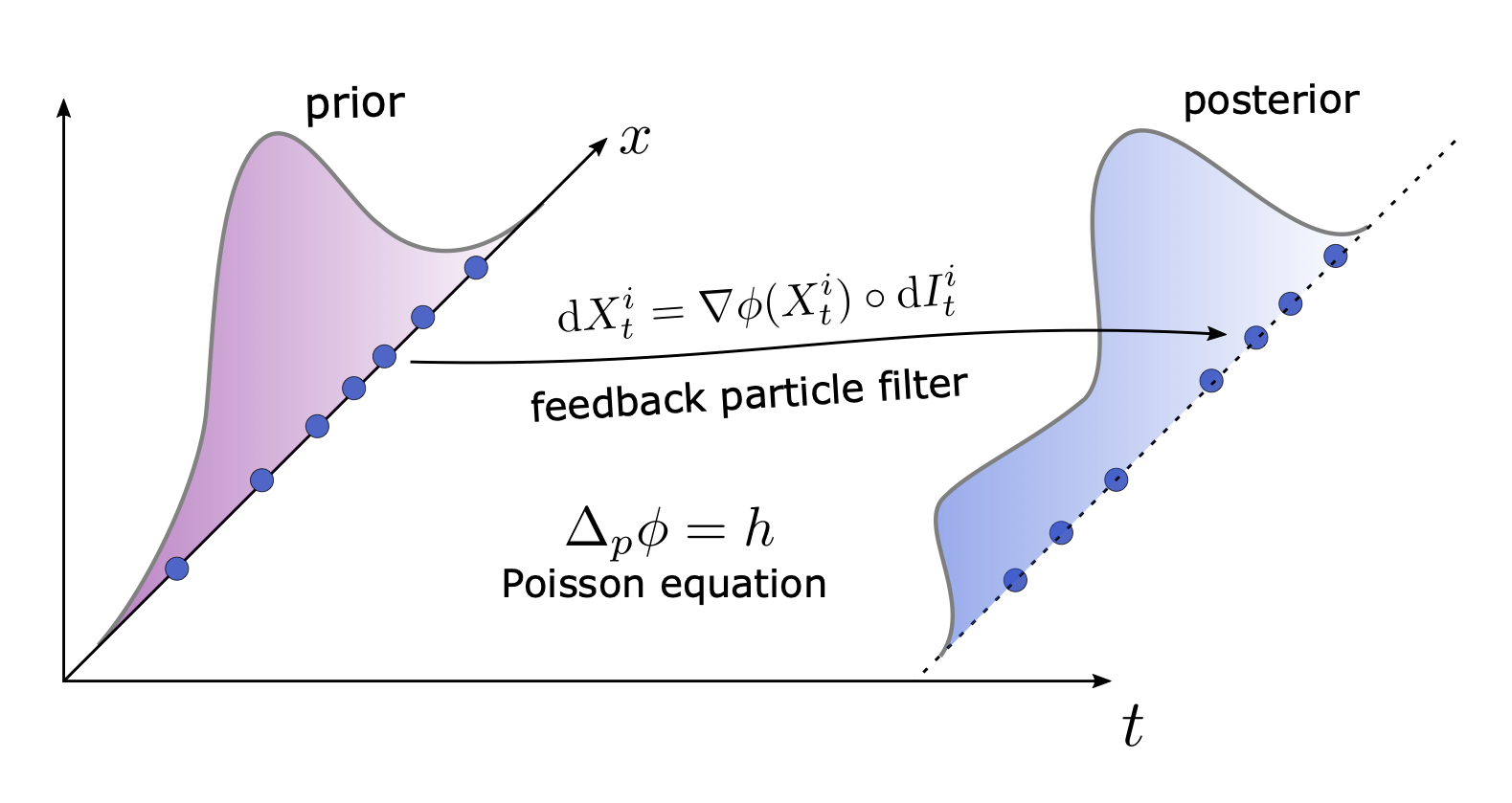
Publications: